¿El mal profesor?

  

El abuelo de un amigo, que era un excelente profesor, decía que el profesor que suspende a un alumno en verdad se suspende a sí mismo.

 

Hay veces que nos pasan cosas surrealistas. Os recomiendo que leáis hasta el final, los comentarios incluidos. Habrá una solución. Y será la menos esperada, lo veréis.

 

 

 

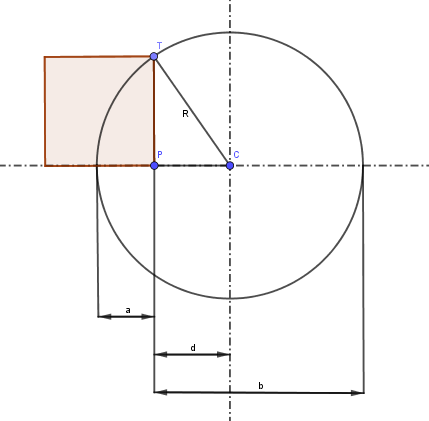
Hoy me han puesto un cero en valores. Una profesora del máster para ser profesor de secundaria nos mandó analizar los valores de un corto, y yo presenté el post que escribí el pasado viernes 13 ( https://calabacitis.blogspot.com.es/2017/10/cosas-que-dan-miedo-que-algunas.html).

Sería por la fecha, pero me han puesto un cero en mi trabajo.

¿Qué esperaría la profesora de nuestro trabajo?

Nos puso dos ejemplos, copio y pego de su guía para hacer la actividad.

 

" Podéis consultar dos ejemplos de guías didácticas en los siguientes enlaces, pero tened en cuenta que son guías sobre largometrajes, por lo que son más extensas de lo que se os pide a vosotros.

Billy Elliot: http://www.aragon.es/estaticos/ImportFiles/09/docs/Ciudadano/CONTS/CONT.01_Mat erialesCursosAnteriores/Creatividad/BILLYPROFE.PDF 

Charly y la fábrica de chocolate: http://www.aragon.es/estaticos/ImportFiles/09/docs/Ciudadano/CONTS/CONT.01_Mat erialesCursosAnteriores/Autoestima/GPROFE+%E2%80%A2+CHARLIE+OK.PDF   "

 

Efectivamente, ninguno de los dos enlaces funcionan.

¿Seré un mal profesor?

No sé.

¡Mira que tener un museo de valores y sacar un cero en mi parte del trabajo de valores!

Parece ser que hay un bulo de que Einstein era mal estudiante.  La idea de que Einstein era mal estudiante parece haber nacido de una confusión de uno de sus primeros biógrafos, al descubrir su etapa escolar en Aarau, Suiza. Cuando Einstein, en 1895, llevó a cabo el examen de acceso al Instituto Politécnico Federal de Zúrich, lo suspendió, en efecto. Pero aparentemente lo hizo porque el examen incluía una prueba en francés, idioma que Einsten no dominaba.

A mí me han puesto un cero no en sueco, ha sido en valores. Y ponía en su rúbrica (con lo que me corregía) que un cero implicaba que no se definen los valores a trabajar o no se ajustan al contenido del cortometraje elegido.

¿Se hará la sueca ella ahora que le he pedido una explicación a ese cero?

Bueno, para consolarme, hoy rescato una entrevista de cuando el que me entrevistaba/evaluaba para ver si lo metía en la revista para la que trabajaba me juzgaba un poco mejor, y llegaba a ver mis valores:

“Mi museo nos transforma de gusanos en mariposas. Aquí se aprende a ser feliz a través de la imaginación”

 

NACHO PASWAL, ARTISTA Y CREADOR DEL AIR MUSEUM, EN LA CALLE CERRO DEL ÁGUILA

 

Al AIR MUSEUM se va para vivir nuestra propia historia. El caleidoscopio que se forma en el camino es el de nuestra propia vida y la vida de los otros. Nacho Paswal ejerce   de anfitrión, de guía y de lúdico chamán en este viaje sin peyote. En el espejo de los dramas personales del artista (la pérdida de sus tres mejores amigos) vemos reflejados los nuestros, nos sentimos cómplices en el dolor colectivo del 11M, del accidente aéreo de Spanair o vibramos con el pulpo Paul en el Mundial de nuestros sueños.

Todo está dentro del indio Mocaqua, el llanto y la risa, la felicidad y la tristeza. Es en ese cuadro donde empieza un cuento en el que Nacho se acabará convirtiendo en la tortuga Casiopea, aquel personaje que guiaba a Momo con sus conchas de luz en la obra de Michael Ende. Si en el Mar de la Imaginación, un museo que se encontraba en la Avenida de Madrid, el elemento era el agua, el AIR MUSEUM, en el Cerro del Águila (al lado del estadio de fútbol Matapiñonera), juega con el aire. Con el aire y el collage de nuestra vida que se convertirá, de triste calabaza, en alegre carroza de cristal. El secreto reside simplemente en dejarse jugar.

 

Te llamas Nacho Muñoz pero tienes otros nombres artísticos como Nacho Paswual y también te dicen el indio Mocaqua. ¿A qué se debe esta proliferación?

 

Lo de Nacho Paswal viene de una anécdota muy divertida. Una novia con la que me carteaba casi diariamente durante seis años, había unido la “c” y la “u” convirtiéndola en una “w” y se pensaba que ése era mi apellido. Así que en uno de los viajes que hicimos sacó un billete de avión con ese nombre en México. Menos mal que era un vuelo interior y no me pidieron documentación.

Me gustó y fue así cómo nació el nombre Nacho Paswual. Además, exorcizaba el hecho curioso de que en mi clase hubiera un Nacho Muñoz… del Toro. Él era el toro y yo era la vaca, ya sabes por lo de la marca de leche “Pascual”.

De esta forma, Paswal era la calabaza convertida en carroza de cristal que curaba eso y además tiene que ver con el mestizaje de culturas, que me encanta. Por otro lado, el indio Mocaqua es el cuadro del que ha surgido todo mi arte y el principio del viaje en este museo.

 

¿Te consideras un artista metido a ingeniero de Caminos o un ingeniero de Caminos metido a artista?

 

Cuando tenía 26 años me di cuenta de que, más allá de lo que quisieran mis padres, tenía un don particular que tenía que desarrollar. Soy y me siento artista. De hecho, en mi arte abogo por romper el tópico de que los artistas sean ciudadanos de tercera y otras profesiones tengan una muy buena reputación, algo que está muy extendido en este país. Más que una profesión, somos personas.

 

¿En qué o quién, cosa, persona, objeto o animal te inspiras para tus creaciones?

 

Todo me inspira, cualquier cosa es susceptible de sufrir el virus de la “calabacitis”. Creo que ese es el truquillo para que esta vida tenga un jugo especial. Lo que hago con mi arte es un collage de vida. Este arte lo que hace es inspirar a otras personas a crear su propio arte. Tiene que ser algo cercano, que te “toque”, para convertir tu propia vida en arte. Este museo es un buen ejemplo: un “loft” de sólo 60 metros se convierte en un espacio de imaginación. Eso es una de las cosas que se muestran aquí: que cualquier persona puede ser artista de su propia vida.

 

El espacio en el que nos encontramos es el AIR MUSEUM. ¿Qué le dirías a la gente para que viniera a verlo?

 

Pues que se paren un momento a pensar el plano tan corto en el que estamos viviendo la realidad.

Vivimos con la idea de superprotección en un mundo cada vez más aséptico. Pero cada vez hay más alergias y surgen enfermedades nuevas.

Este museo lo cura todo, nos transforma de gusanos en mariposas. Aquí se aprende a ser feliz a través de la imaginación.

 

¿Consideras el arte como un viaje? ¿Hacia dónde?

 

Es un viaje que me plantea un reto: cualquier obra, cuadro, escultura, objeto está relacionado con los otros y tiene su sentido de ser en esa relación. Yo no vendo cuadros, no tendría sentido poner un cuadro mío en el salón. Por otro lado, ese viaje en el que yo hago de guía de los espectadores es una experiencia de aprendizaje a la manera de los cuentos de hadas. A pocas personas como a mí se le mueren en tan corto lapso de tiempo sus tres mejores amigos, los que más habían influido en mi vida. Yo he convertido poco a poco, con mi arte, este drama en una experiencia positiva, llena de luz e imaginación.

Este museo lo he ido haciendo en 14 años y montando finalmente en uno. Es un arte muy distinto a todo lo que se hace habitualmente.

 

¿Qué significa para ti el reciclaje?

 

Trabajo con elementos ya usados, de la basura…Para mí es también es una manera de convertir cosas que tenían otro uso o ya no sirven en elementos de mi universo, cada uno con un significado propio e integrado en un todo. Es una forma de sublimar la realidad a través de la magia del arte. Para mí el reciclaje es una filosofía de vida. Aquí hay pintura de tren porque tiene que ver con los hechos trágicos del 11 M, también pintura que había pasado por el fuego de un Leroy Merlín que se quemó… Los materiales con los que trabajo importan, tienen historia. Para mí el significado es sacar, de la basura, algo bello.

 

¿Le has dado otra vuelta de tuerca al concepto de “loft” o lo de haber elegido este loft ha sido pura circunstancia?

 

Este “loft” se encuentra en la calle Cerro del Águila y su elección tiene que ver con ese mito medieval en el que el águila, a la mitad de su vida, se marcha a un cerro para arrancarse sus plumas viejas y el pico, y esperar a que le nazcan otras nuevas. Es un lugar que abre los ojos a la vida, a la auténtica vida.

 

Nieto como eres de agricultor, has dicho que tu hortaliza preferida es la calabaza, por ese carácter mágico de cuento que tiene. ¿A quién te gustaría dar calabazas?

 

Por ejemplo, al canal Gran Hermano 24 Horas que acaba de sustituir al recién extinguido CNN+. Es una gran metáfora de lo que está ocurriendo en España. Ocurren estas cosas y parece que no pasa nada. Nos hemos convertido en seres pasivos. Parece que cada vez cuesta más moverse. Me da mucha pena. Una de las cosas que trato con mi arte es que la gente abra los ojos, que despierte. De esa forma, la calabaza se convierte en carroza.

 

Imagina que tienes a tu disposición todo San Sebastián de los Reyes. ¿Qué tipo de proyecto creativo harías?

 

Haría el que he hecho. Fíjate que desde aquí se ve el Plaza Norte, que es como un mausoleo y que en un momento dado también forma parte del viaje. El AIR MUSEUM es como su contrapunto, un espacio para pensar y divertirse siendo creativos. Hablamos de 14 años de trabajo. Este es un arte filosófico que tiene que ver con cada uno de nosotros. Hay museos temáticos, pero este es un museo de vida.

Cualquier persona, adulto o niño, de cualquier condición, es protagonista y parte fundamental de este viaje. Como en la vida, hay momentos de alegría, de dolor y al final de renacimiento.

 

Siendo como eres de Sanse, ¿qué te parece el gran cambio que ha dado en las últimas décadas?

No todo ha sido para bien. San Sebastián de los Reyes se está convirtiendo en una ciudad. Yo la he vivido cuando era un pueblo. Me acuerdo cuando, de pequeño, Pepe Hierro (el poeta que da nombre a la Universidad Popular) me hablaba cuando venía. En Sanse la cultura era muy importante para los vecinos. Ahora somos cada vez más pasivos. Y, sin embargo, hay oportunidades.

A mí, por ejemplo, me enseñan Tai-chi gratis todos los lunes y los miércoles en el Centro Actúa. Hay que aprender a no andar en carriles, a quitarse las orejeras. Sanse nació como un acto de sublevación frente al señor feudal de turno y pidió amparo a los Reyes Católicos para crear este espacio de libertad. De aquello hoy también podemos aprender mucho. Para estar vivos hay que recuperar la lucidez y ésta nos traerá la libertad.

Y me despido con un vídeo del museo y un enlace a otra entrevista en él (que también seguirá mostrando valores):


https://www.youtube.com/watch?v=vMGaw9YSnXs

https://www.youtube.com/watch?v=6zlkmaBMR7Y

El lobito bueno que elegí de fondo

Esta leyenda Cheroqui me inspiró para pintar el cuadro. Siempre estará vigente, y lo mismo sirve para un país que para un individuo, aunque sea éste del mundo occidental. Merece la pena recordarla de vez en cuando.

Un viejo indio estaba hablando con su nieto y le decía:

“Me siento como si tuviera dos lobos peleando en mi corazón. Uno de los dos es un lobo enojado, violento y vengador. El otro está lleno de amor y compasión”.

El nieto preguntó:

“Abuelo, ¿cuál de los dos lobos ganará la pelea en tu corazón?”.

El abuelo contestó:

“Aquel que yo alimente”.

El eje radical y problema fundamental de tangencia explicado por Quelo

  

 

 

 

Hoy , con todo lo del artículo 155 de por medio, Quelo, que sabe distinguir entre lo razonable y lo inmoderado, nos va a presentar el concepto de lo que es un eje radical.  El eje radical de dos circunferencias no concéntricas, es el lugar geométrico de los puntos con igual potencia respecto  a ellas. Éste en particular, es tan radical que muestra claramente que todo es blanco o negro para él.

 

 

 

 

Hoy, con este concepto ya entendido,

, vamos a resolver el problema fundamental de tangencias con un eje radical. Y lo haremos por pasos.

¿Habrá sólo una solución? ¿O habrá dos? Vamos a ver, por si acaso:

(Y un pequeño detalle que también nos explica Quelo: la disposición de los colores de la bandera de la Paz está invertida con la bandera del colectivo LGTB).

Bueno, ¡a ver si sale el arcoíris ahora que sabemos las dos soluciones de este problema!

Las cabezas cuadradas

Hoy he recuperado este CorreoCaminos de 1996. Hace ventiún años, en la misma Escuela de Caminos donde hoy hago un máster para ser profesor de secundaria de expresión gráfica, YO ARMÉ UNA REVOLUCIÓN. Los profesores pretendían que sólo fuéramos ingenieros, que dejáramos de un lado lo de ser hombres. Todo tenía que ser estudiar, y hasta nos querían concentrar los exámenes para que no pudieramos más que ir a curso por año, pues si no se nos montaban...

Yo llené la Escuela Gris de Color, con mi primera exposición, que se tituló "10 poesías, 10 cuadros y 10 fotografías y no 30 exámenes en 10 días". Estaba en segundo de carrera por entonces y la lie parda. ¡¡¡Y vencimos!!! Fue mi primera exposición, pero no creo que haya otra de la que me sienta más orgulloso en mi vida.

Bueno, por entonces me creía que todo aquello que pasaba con los profesores era porque estudiábamos ingeniería. Pero no, veintiún años más tarde sé ya que el ser humano es así, se estudie lo que se estudie. Hoy me encuentro con profesores de asignaturas que deberían de ser bonitas, que deberían de tener al alumno en cuenta, que ya no sólo son ingenieros, que los hay incluso psicólogos, pero que siguen tan cabezas cuadradas. ¿Son distintos? No. Nos quieren enseñar a ser profesores así, a lo burro. Concentrando mil tareas y exámenes en 30 días, no pensando más que en el prestigio de su máster, no teniendo nunca en la cabeza facilitar la tarea al alumno...

Hoy voy a pedir dos deseos: el primero es que el día que yo sea profesor, respete el tiempo del otro para ser persona también.

Y el segundo, como hoy va la cosa de mentes cuadradas, que España cambie. Y es que valoro y presumo en el extranjero de la riqueza cultural de España; en paisaje, gastronomía, lenguas, costumbres, hasta razas. Pues somos una mezcla de tanto: celtas, iberos, tartesos, judíos, moros... No soporto los nacionalismos, ni de un lado ni de otro. Tanto escozor me provoca la actitud intolerante de los extremistas catalanes, como los que enarbolan orgullosos, como únicos poseedores, la bandera de España, igual de intolerantes. Esas actitudes, las de no respeto a los demás, son las que dan miedo, las que provocan y han provocado guerras, y sinceramente, vergüenza. Por un país tolerante, diverso, culto y respetuoso con las diferencias, y que, en lugar de concentrar exámenes para ser español o catalán, sea capaz de dejar al otro vivir. Que tanta bandera ya aburre y que no cambien nunca las cosas... más todavía.

Un mar de imaginación para cuando te canses de caminar por el suelo

"Las personas deben hablar menos y dibujar más. Personalmente, me gustaría renunciar por completo del habla y, al igual que la naturaleza orgánica, comunicar todo lo que tengo que decir visualmente"

Johann Wolfgang Von Goethe

 

 

 

Y aquí un vídeo que demuestra el teorema de Johann Wolfgang Von Goethe:

 

un mar de imaginación para cuando te canses de caminar por el suelo

Problema fundamental de tangencias (en la vida y en el papel)

  

   En mi profesión de ingeniero civil no son pocas las veces que he escuchado a alguna persona decir que su vida no tenía sentido o que no le encontraba sentido a la vida. Yo mismo, trabajando en alguna empresa que no me respetaba como persona, sentí que debía dar un giro de 180 grados para encontrarlo. O encontrar una circunferencia tangente a ésa que era la de la ingeniería que pasara por dos puntos que me apasionaban. Fue así que acabé queriendo ser profesor de expresión gráfica y artista.

   Esta búsqueda universal de "el sentido de la vida" no suele verse satisfecha fácilmente y, a mi parecer, en gran parte se debe a que la vida, como concepto, es demasiado subjetivo para encontrarle un único sentido que nos saque de nuestra habitual incertidumbre. 

   Yo prefiero plantear la pregunta de otro modo: 

    ¿Cómo puedes tú darle sentido a tu vida?,

    ¿Qué puedes hacer tú?,

    ¿Qué depende de ti?

   Para responder a estas preguntas entiendo que podemos darle "sentido" a nuestra vida al menos en tres aspectos diferenciados.

   "Sentido" en cuanto a dirección. ¿Hacia dónde te diriges? ¿Qué dirección le estás dando o quieres darle a tu vida? Supone asumir la responsabilidad de hacer con tu vida lo que realmente quieres o al menos intentarlo. Ser coherente con uno mismo y, por tanto, tratar de que nuestro pensar, nuestro sentir y nuestro hacer vayan en una única dirección.

   "Sentido" en cuanto a significado; ¿Qué significa la vida para ti?, ¿la ves como un valle de lágrimas donde uno viene a sufrir? o, más bien como una oportunidad de crecimiento?. El significado que le das a la vida es tu responsabilidad también porque va a condicionar tus expectativas respecto a ella y , en gran medida, la dirección que le des.

   "Sentido" en cuanto a "sentir", a estar vivo o, lo que es lo mismo, a valorar el momento presente viviéndolo conscientemente, dándole valor a lo que esta ocurriendo ahora, a este único momento donde existe la vida más allá de lo conceptual, la vida como experiencia actual, la vida como presencia.

   No malgastes más tu tiempo buscándole sentido a tu vida como quien busca una aguja en un pajar, en vez de eso concéntrate con todas tus fuerzas en dárselo tú porque, entre otras cosas, solo tú puedes hacerlo.

   Por otro lado, no conozco una forma mejor de encontrar aquello que buscas que dándolo, dándotelo.

¡A por ello!

   Yo quiero ser profesor, pero de otra forma distinta a la mayoría de los profesores con los que me he encontrado en mi vida. En la pedagogía tradicional el esfuerzo está asociado al dolor, al malestar, y a la idea de que adquirir conocimiento tiene que ver con la ansiedad, el miedo o la evaluación. Mi propuesta es incorporar el arte en la educación para generar placer y de esa forma conseguir que el esfuerzo y la constancia aparezcan de forma automática. Los calabazos me ayudan a encontrar ese sentido y esa dirección, si me pierdo de nuevo ahí estarán, guiándome.
 

 

 

   Vimos en otro post, el de potencia con amor, unos cuantos conceptos. No era para ser evaluados con miedo. Sólo eran semillitas que ahora veréis sus frutos. Nos los traía Fili, ¿recordáis? Venga, juguemos a abrir los ojos. Mirad que los ojos de Fili pueden ser representados por dos circunferencias tangentes. ¿Os atreveríais a relacionar todas esas semillitas de potencia con amor con un problema fundamental de tangencias?

¡Qué sí, hombre/mujer! Que en la vida los problemas pueden ser una oportunidad de crecimiento. ¡Vamos a verlo con este vídeo de youtube!

 

 

 

Cosas que dan miedo que a algunas personas les de miedo

   Hoy es Viernes 13 y a mí hay cosas que me dan miedo. Os voy a presentar un corto que por supuesto que no he hecho yo, ¡ya me gustaría a mí! Al final entenderéis qué me da miedo. Os animo a, antes de leer el resto de mi post, buscarlo en youtube.¡Venga, que seguro que a vosotros no os da miedo! De veras, es un cortometraje genial. Se llama "In a Heartbeat".

   “In a Heartbeat” (“En un latido”), en solo cuatro minutos,  promueve la tolerancia y el respeto trasmitiendo un mensaje de amor y aceptación para los niños que sienten que no encajan en el patrón sexual que la sociedad les impone. Muestra qué es lo que llevan por dentro al vivir con temor a sus sentimientos y a que todos los demás sepan que no encajan en ese patrón. Explica desde una mirada sensible y natural la sexualidad de dos niños. Normaliza su homosexualidad, mostrando que los sentimientos son los mismos y el amor que puede sentir un niño por otro es exactamente el mismo que el que sentiría un niño por una niña o viceversa. Hace ver al mundo (sin imponer nada, sólo mostrándoles algo que ocurre) que todos tenemos el derecho de sentir amor puro y de elegir a la persona con la que queremos estar (independientemente de edades o géneros). Muestra que quizás ese amor pueda ser correspondido, y cómo quizás no debemos tener miedo de seguir nuestras elecciones sexuales, ni siquiera en edades tempranas. El mensaje transgrede los prejuicios sobre la comunidad LGBTI y la hipersexualización que a menudo se le ha dado a este colectivo.

   Sin diálogos y sin una historia compleja, se muestra la relación entre dos chicos, que se convierte en un poderoso recurso para desmontar prejuicios y demostrar que no existe una sola manera de vivir el primer amor, que los flechazos de instituto no son solo heteros.

   Un chico observa a escondidas al amor de sus sueños cuando, de repente, literalmente, se le sale el corazón para perseguirlo dentro de las instalaciones de su escuela, sin que pueda controlarlo. El chico enamorado lucha para tratar de contener a un sonriente e intrépido corazón, sintiendo el peligro de que el otro se percate de sus sentimientos y de que el resto de la sociedad pueda atisbar ese amor. El mensaje no se impone, pero es claro por mera reflexión interna: no hay nada malo con esos sentimientos, no hay razones para ocultarlos. Los nervios, temores e inseguridades del primer amor son iguales a los del primer amor entre personas de distinto sexo aparte de ese deseo del personaje principal de que pase desapercibido.

   El corto va más allá de lo que estamos acostumbrados a ver porque aborda el tema sin enmascarar nada. La escena con los compañeros dentro del colegio logra representar con profundidad la crudeza y los prejuicios de una sociedad que en situaciones así opta a menudo por discriminar y criminalizar (como si hubiese algo malo detrás). Pocas veces, y mucho menos en un cortometraje destinado también al público infantil, se ha visto un tratamiento al tema tan profundo, coherente y respetuoso. Es un cortometraje que todos los niños deberían ver, para que puedan comprender la lucha del protagonista por expresar lo que siente y no repetir esa criminalización llegado el momento, si se les presenta la situación de presenciar algo parecido. El visionado por un niño o niña que se encuentre en una situación parecida a la del personaje principal le ayudará a no sentirse tal “bicho raro”, a que pueda desarrollarse como persona sin ninguna “olla a presión que pueda explotar en su cabeza”. Si este corto se dirige únicamente a los adultos, pierde gran parte de su fuerza y capacidad transformadora. Y es que el tema de la homosexualidad debería normalizarse; el día que las personas no hagan de él un escándalo, todos ganaremos, incluso los que todavía no se han puesto a pensar que criminalizar a alguien por sus elecciones sexuales quizás sólo lleve a que el efecto Pigmalión se cumpla, lo cual es muy peligroso también para ellos.  Explicar desde una mirada sensible y natural la sexualidad de dos niños, promoviendo la tolerancia y el respeto, es el primer paso para que todo esto cambie.

   Por supuesto, como era de esperar, a pesar de ser un cortometraje que sólo muestra una realidad presente y de la forma más luminosa y natural posible,  no ha escapado a las controversias, generando un debate entre algunos sectores muy determinados que hasta lo llegan a acusan de difundir la homosexualidad entre los menores y manifiestan su oposición a que sea mostrado en un aula.  En esos sectores se tiene la opinión de que se les estaría imponiendo una ideología homosexual a los niños que lo visionaran, ya que su opinión sobre el respeto a la diversidad y  enseñar a los niños a no discriminar va por otro lado. Este corto en las aulas seguramente lo considerarían una imposición inaceptable. ¿Por qué les preocupa mostrar una realidad sobre la orientación sexual? ¿Acaso hay algo inherentemente malo en ser gay/lesbiana/ bisexual o trans? Los cuatro minutos de cortometraje para algunos son tremendamente peligrosos, ya que posiblemente desmontan sus argumentos sin decir ni una sola palabra ni imponer nada al espectador. Desmonta argumentos de esos sectores contra la teoría de género, los que apelan a la experiencia cotidiana (por ejemplo a ver como los niños y las niñas pequeñas presentan diferencias naturales y se manifiestan y actúan de modo distinto). En estos cuatro minutos sin palabras se ve una realidad universal, que es que no todos los niños son iguales, y eso resulta inaceptable para unos cuantos.

   ¿Por qué esos sectores ven el corto como una herramienta para difundir la homosexualidad? ¿Quizás porque hay un final en el que el amor es correspondido? Se ha mostrado lo difícil que ese niño tiene en su interior aceptar algo que está sintiendo, sin caer tampoco en nadie diciéndole que eso que siente está bien o mal. ¿Cambiar el final en el que el amor es correspondido haría que esos sectores no opinaran lo mismo? ¿o es que para proteger de lo que ellos llaman la difusión de la homosexualidad se debe nunca poder hacer reflexionar a alguien sobre lo que está ocurriendo dentro de un ser que está inspirado en lo que los propios autores del corto han sentido, como tanta gente en el mundo? Y es que el cortometraje, por mucho que esos sectores se empeñen en intentar censurarlo, analiza el tema de una forma blanca, casi como si fuera un documental, sin caer en recursos que podrían dar rienda suelta a que esos sectores pudieran decir lo que dicen con fundamento. El tema está tan bien tratado que resulta increíble que alguien pueda llegar a estar en desacuerdo de que se pueda mostrar en un aula.

No os he presentado todavía formalmente a Trompo (que ya veréis que contagia sencillez), ni a Croco (que ya veréis que contagia realismo).  Pero sí, ya conocéis a Manatito y a Urso. ¿Por qué los traigo a todos juntos con el corto? Porque ellos cuatro y yo hemos visto juntos "In a Heartbeat". Y nos ha encantado de qué manera tan sencilla y real trata el tema del amor entre dos personas del mismo sexo. Y los cinco hemos soñado juntos, tras su visionado, que este corto abra un poquito las mentes para que dos personas así no se sientan nunca desprotegidas por simplemente sentir. Y ojalá que esa sociedad que antes no entendía amores así, pueda abrir los ojos y, como Manatito, alegrarse si tiene un final feliz.

   

Potencia con mucho amor

El amor es pura potencia. Teniendo amor podrán venir el resto de fuerzas que nos traigan la felicidad. Hoy Fili se va a encargar de recordarnos algunos conceptos geométricos, pero antes vamos a dejar que nos recuerde (esta vez en inglés, que es el idioma universal hoy en día) lo potencial que es el amor.


Por cierto, Mocaqua es el alter ego de Calabazo Mayor del Reino (o del artista Nacho Paswal). Eligió ese nombre porque es pura potencia, ya que significa de alguna forma "mi agua" (y ya sabes que somos un 80% agua pura).


Bueno, ahora, que lo hemos recordado, estamos preparados para todo lo demás.



Concepto de Potencia de un punto P respecto a una circunferencia (me da igual que el punto sea interior o exterior a la circunferencia): es el producto de la distancia mayor por la distancia menor del punto a dicha circunferencia c.

¿Si hablamos de distancias a un punto, en verdad de qué estamos hablando gráficamente? De circunferencias de centro ese punto. Si empezáramos a trazar circunferencias de centro P, habrá una que sea tangente a la circunferencia c. La tangente común a las dos circunferencias es perpendicular a los radios, y como los radios están alineados, sacamos que a es la distancia menor y b es la distancia mayor ( ambas distancias se encuentran en la prolongación del diámetro que pasa por el punto P).


La distancia del punto P al centro de la circunferencia es d

Podemos expresar que a= d-R y b= d+R


si multiplicamos a * b = (d-R) * (d+R)

y como suma por diferencia es diferencia de cuadrados

a * b =d² - R²

que nos recuerda a la expresión de un cateto despejado del teorema de Pitágoras

d² - R²  = W² 

donde  d² = W² + R²       siendo d la hipotenusa, R un cateto y W el otro cateto. 

Si d es la hipotenusa, los catetos tienen que estar en un arco capaz de 90º



Donde se intersecte el arco capaz con la circunferencia c tendré el vértice del triángulo rectángulo que tiene un cateto que mide R y otro que mide W.


 

Llamamos a W raíz de la potencia (a W al cuadrado le llamaremos potencia). Recuerda que potencia es por definición el producto de dos distancias, y para que las dimensiones a ambos lados de la igualdad cuadraran, hemos decidido hacerlo así.


Luego la raíz de la potencia (W) de un punto exterior a una circunferencia es el segmento de tangencia.


¿Qué sería entonces la potencia? El área del cuadrado de lado W (cuyos vértices son M1,L1, P y el punto de corte del arco capaz con la circunferencia ).

Ahora vemos cómo sería si el punto P fuera interior a la circunferencia:



La potencia de un punto P respecto de una circunferencia es igual a la diferencia de cuadrados de la distancia del punto P al centro C de la circunferencia y el radio R de la misma y también al cuadrado del segmento de semicuerda PT perpendicular a PC si P es interior

Es decir, la potencia en este caso sería el área del cuadrado rosa:

Generalización del concepto de “Potencia”


Si consideramos dos rectas que pasan por un punto P y seccionan a una circunferencia, los puntos de corte con dicha circunferencia (A, B, C y D) determinan dos triángulos semejantes:


PAD
PCB

Al aplicar los conceptos de arco capaz sobre un segmento, vemos que los ángulos en B y D deben ser iguales por ser inscritos en la circunferencia que pasa por los cuatro puntos. Por otro lado los triángulos comparten el vértice P y por lo tanto su ángulo, y en consecuencia son semejantes.


Aplicando el teorema de Thales a los dos triángulos semejantes tendremos que:

PA/PD = PC/PB


y por lo tanto


PA * PB = PC * PD = Constante


Lo que demuestra que la potencia desde el punto P es independiente de la recta elegida, como queríamos demostrar.

Sólidos platónicos

      Como Fili contagia amor, le apasionan los sólidos platónicos. Y mucho más si son azules, no lo puede evitar. Se ha puesto a contar en azul (que no es lo mismo que contar en verde) y fíjate toda la información valiosa que ha sacado:

 

 

 

 

Un día te contará el secreto de cómo ha hecho la tabla, que ha sido mentalmente.

 

 

 

      Los sólidos platónicos son poliedros regulares y convexos. En todos los vértices concurren el mismo número de caras y aristas. A los calabazos les hubiera encantado que fueran diez, para quedarse uno cada uno, pero son cinco, sólo cinco. Es por eso que, entre todos, han pactado que sea Fili el que los guarde bien. Fili ha decidido congelarlos, para que no se les derrita ni una arista, ni un vértice, ni una cara. En verdad es por eso que son azules los de Fili, sólo porque están congelados. Pero a veces descongela alguno y los pinta de otros colores, no te creas. Al ya estar descongelados, puede entonces suceder que, cuando cuentes sus aristas, sus vértices o sus caras, no te de justo-justo los de la tabla. No lo dudes entonces, habrán dejado de ser platónicos y habrán ya caído en la monotonía del día a día.

 

 

Manatito convertido en agua nos trae a Pitágoras

Para definir la forma de un cuadrado, ¿cuántos datos necesito? Ninguno. La forma está definida.

Para definir la forma de una circunferencia, ¿cuántos datos necesito? Ninguno. La forma está definida.

Para definir la forma de un triángulo, ¿cuántos datos necesito? Dos.
Un triángulo tiene tres ángulos y tengo una ecuación que me los liga: la suma de los ángulos interiores de un triángulo es pi radianes, o 180 grados sexagesimales, o 200 grados centesimales

¿Y si el triángulo fuera rectángulo? ¿Cuántos datos necesito para definir su forma? Pues como sé que uno de los ángulos es recto, ya sólo necesito un dato más.


Ahora Manatito te va a enseñar algo mágico que cumplen los triángulos rectángulos, que es el teorema de Pitágoras. Y lo hará convertido él en agua, con un vídeo que seguro que te lleva a entenderlo maravillosamente:

                                    vídeo de https://www.youtube.com/watch?v=1er3cHAWwIM 


 En un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Efectivamente, si sumamos las áreas de los cuadrados construidos sobre los catetos, nos da el área del cuadrado construido sobre la hipotenusa.


¿No es genial? Bueno, y ahora sólo me queda enseñarte a Manatito convertido en agua:

El teorema de Thales

 

 Escultura bien moderna de Thales de Mileto (ca. 630-545 a.C.) sobre base de mármol Manatítico

                           

Bueno, ahora ya en serio (que Manatito no sólo es alguien con quien reír, sino también alguien con quien aprender):

El primer teorema de Thales establece que si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que  es semejante al triángulo dado (relacionando la longitud de dos de sus lados). Permite definir un invariante proyectivo de aplicación a los sistemas de proyección cilíndricos: La razón simple.

Si cortamos dos rectas cualesquiera por varias rectas paralelas,los segmentos correspondientes en ambas son proporcionales,es decir, se corresponden en la igualdad ,en la suma y en la resta.
 

 

 

 

 

 

El teorema establece las siguientes igualdades entre los cocientes de dos lados homólogos en dos triángulos semejantes:

• m/n = m’/n’
• m/n = (m+m’)/(n+n’)
• n/p = (n+n’)/p’

¿Tú querrías que Thales te llevara a un mundo nuevo? Pues déjate llevar, que esto no tiene límites. Si de tal palo tal astilla... ¿has visto que Thales está hasta en las sombras? Empecé mi exposición del teorema de Thales con un Manatito juguetón que quería fusionarse de alguna manera con Thales. La termino con el padre de la criatura jugando con las sombras, jugando también artísticamente con Thales (en una foto que tomó del paraíso):