El amor es pura potencia. Teniendo amor podrán venir el resto de fuerzas que nos traigan la felicidad. Hoy Fili se va a encargar de recordarnos algunos conceptos geométricos, pero antes vamos a dejar que nos recuerde (esta vez en inglés, que es el idioma universal hoy en día) lo potencial que es el amor.
Por cierto, Mocaqua es el alter ego de Calabazo Mayor del Reino (o del artista Nacho Paswal). Eligió ese nombre porque es pura potencia, ya que significa de alguna forma "mi agua" (y ya sabes que somos un 80% agua pura).
Bueno, ahora, que lo hemos recordado, estamos preparados para todo lo demás.
Concepto de Potencia de un punto P respecto a una circunferencia (me da igual que el punto sea interior o exterior a la circunferencia): es el producto de la distancia mayor por la distancia menor del punto a dicha circunferencia c.
Por cierto, Mocaqua es el alter ego de Calabazo Mayor del Reino (o del artista Nacho Paswal). Eligió ese nombre porque es pura potencia, ya que significa de alguna forma "mi agua" (y ya sabes que somos un 80% agua pura).
Bueno, ahora, que lo hemos recordado, estamos preparados para todo lo demás.
Concepto de Potencia de un punto P respecto a una circunferencia (me da igual que el punto sea interior o exterior a la circunferencia): es el producto de la distancia mayor por la distancia menor del punto a dicha circunferencia c.
¿Si hablamos de distancias a un punto, en verdad de qué estamos hablando gráficamente? De circunferencias de centro ese punto. Si empezáramos a trazar circunferencias de centro P, habrá una que sea tangente a la circunferencia c. La tangente común a las dos circunferencias es perpendicular a los radios, y como los radios están alineados, sacamos que a es la distancia menor y b es la distancia mayor ( ambas distancias se encuentran en la prolongación del diámetro que pasa por el punto P).
La distancia del punto P al centro de la circunferencia es d
Podemos expresar que a= d-R y b= d+R
si multiplicamos a * b = (d-R) * (d+R)
y como suma por diferencia es diferencia de cuadrados
a * b =d2 - R2
que nos recuerda a la expresión de un cateto despejado del teorema de Pitágoras
d2 - R2 = W2
donde d2
= W2 + R2 siendo d la hipotenusa, R un cateto y W el otro cateto.
Si d es la hipotenusa, los catetos tienen que estar en un arco capaz de 90º
Donde se intersecte el arco capaz con la circunferencia c tendré el vértice del triángulo rectángulo que tiene un cateto que mide R y otro que mide W.
Llamamos a W raíz de la potencia (a W al cuadrado le llamaremos potencia). Recuerda que potencia es por definición el producto de dos distancias, y para que las dimensiones a ambos lados de la igualdad cuadraran, hemos decidido hacerlo así.
Luego la raíz de la potencia (W) de un punto exterior a una circunferencia es el segmento de tangencia.
¿Qué sería entonces la potencia? El área del cuadrado de lado W (cuyos vértices son M1,L1, P y el punto de corte del arco capaz con la circunferencia ).
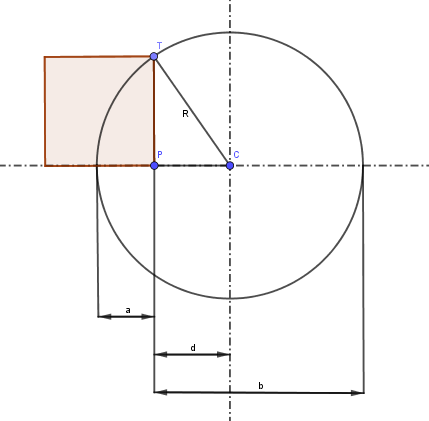
Ahora vemos cómo sería si el punto P fuera interior a la circunferencia:
La potencia de un punto P respecto de una circunferencia es igual a la diferencia de cuadrados de la distancia del punto P al centro C de la circunferencia y el radio R de la misma y también al cuadrado del segmento de semicuerda PT perpendicular a PC si P es interior
Es decir, la potencia en este caso sería el área del cuadrado rosa:
Generalización del concepto de “Potencia”
Si consideramos dos rectas que pasan por un punto P y seccionan a una circunferencia, los puntos de corte con dicha circunferencia (A, B, C y D) determinan dos triángulos semejantes:
PAD
PCB
Si consideramos dos rectas que pasan por un punto P y seccionan a una circunferencia, los puntos de corte con dicha circunferencia (A, B, C y D) determinan dos triángulos semejantes:
PAD
PCB
Al aplicar los conceptos de arco capaz sobre un segmento, vemos que los ángulos en B y D deben ser iguales por ser inscritos en la circunferencia que pasa por los cuatro puntos. Por otro lado los triángulos comparten el vértice P y por lo tanto su ángulo, y en consecuencia son semejantes.
Aplicando el teorema de Thales a los dos triángulos semejantes tendremos que:
Aplicando el teorema de Thales a los dos triángulos semejantes tendremos que:
PA/PD = PC/PB
y por lo tanto
PA * PB = PC * PD = Constante
Lo que demuestra que la potencia desde el punto P es independiente de la recta elegida, como queríamos demostrar.






Y si es interior a la circunferencia? Entonces no hay tangente ...
ResponderEliminarTu duda, José Juan, era muy interesante. Modifiqué el post para responderla. Espero que te haya quedado claro ahora. Un saludo.
ResponderEliminar